Predictive Models for Heart Disease Diagnosis

End-to-end ML pipeline on BRFSS 2020: data understanding & preprocessing, model selection (Decision Tree, Logistic Regression, KNN, Naïve Bayes), 10-fold CV, and cost-sensitive decision thresholding (FN » FP) tailored to healthcare risk.

Executive Summary
Tech Stack
Data Preparation
Modeling & Tuning
Cost-Sensitive Thresholding
Evaluation
Selected Code
Conclusion & Future Work

Executive Summary

Dataset

BRFSS 2020 (CDC)

Task

Heart disease classification

Split

Train/Test = 60/40 (rs=42, stratified)

Objective

Minimize False Negatives (Recall↑)

Best Model

Logistic Regression after threshold tuning

Tech Stack

Python NumPy Pandas scikit-learn Matplotlib Seaborn

Data Preparation

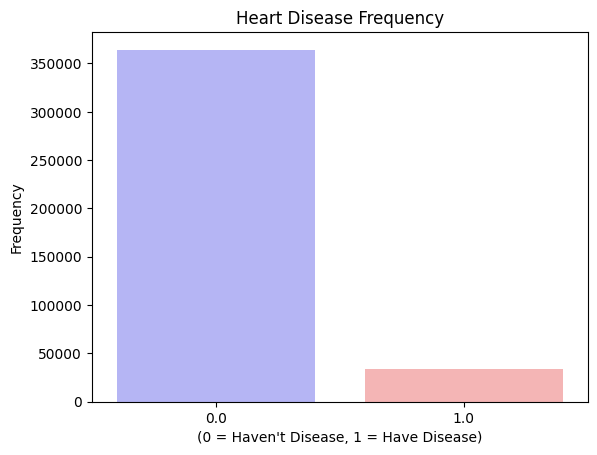
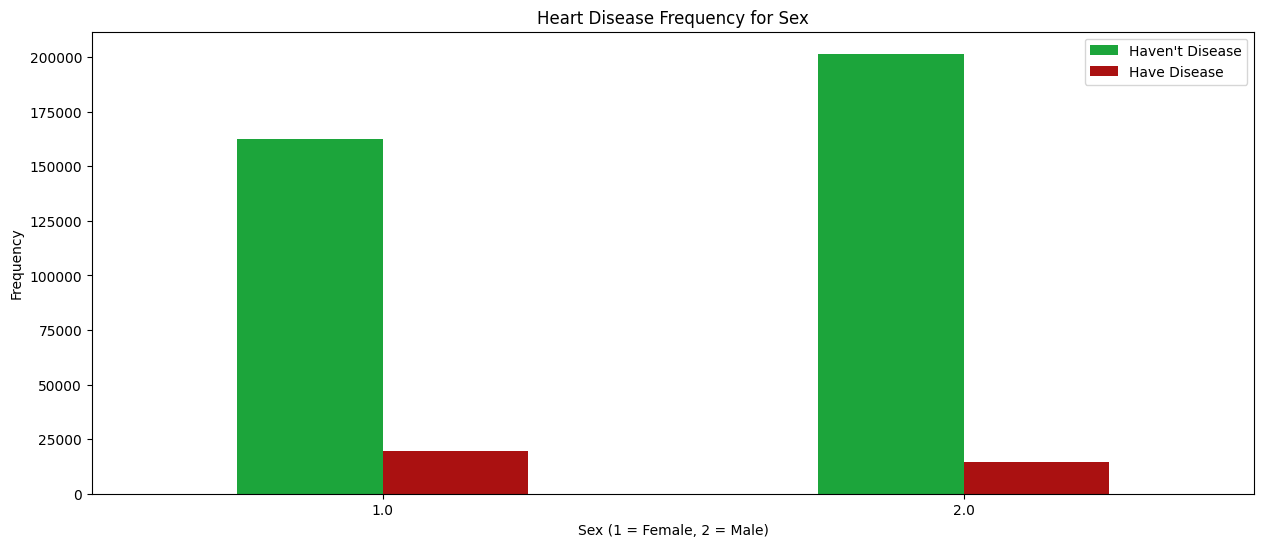
Target: _MICHD (CHD/MI ever; map 2→0).
Cleaning: drop vars >90% null; handle special codes (7/9/77/98/99/777/999); min-max scale numeric; one-hot encode categoricals.
Split: 60/40 train/test, random_state=42, stratified.

Heart disease frequency by sex — Frequency by sex.

Modeling & Tuning

Compare Decision Tree, Logistic Regression, KNN, and Naïve Bayes. Hyperparameters via 10-fold CV with recall emphasis (KNN uses accuracy to avoid k=1 overfit).

Decision Tree: tune max_depth, max_leaf_nodes.
Logistic Regression: penalty='l1', solver='saga', max_iter=2000, grid over C.
KNN: grid over n_neighbors; best around k=8.
Naïve Bayes: Gaussian / Bernoulli based on encoding.

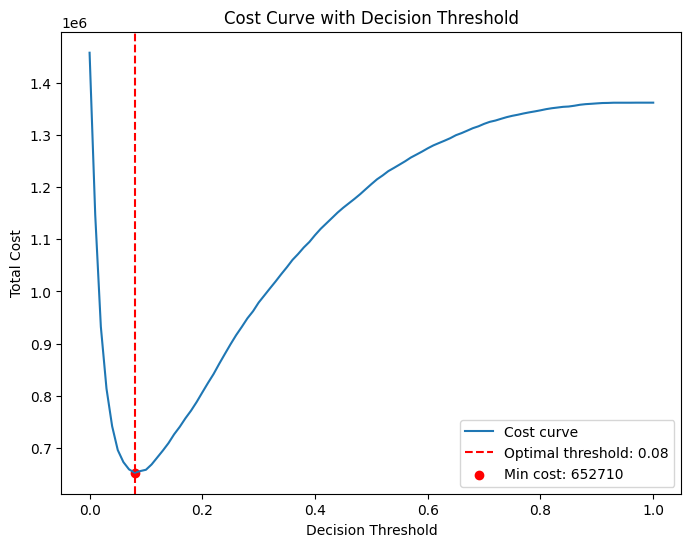
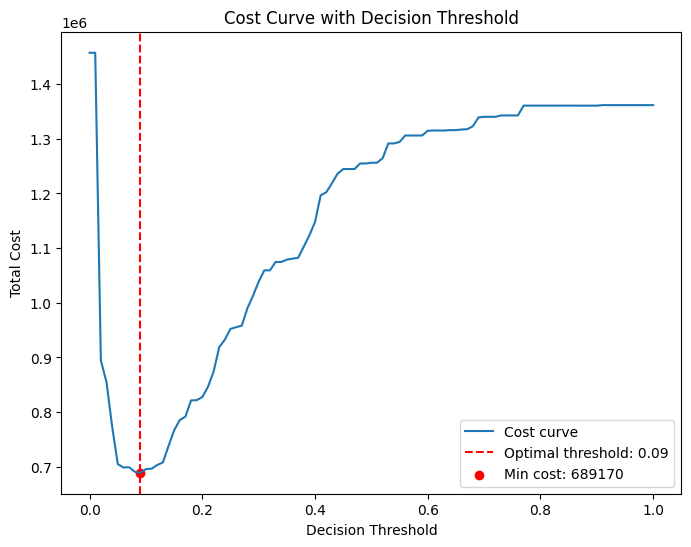
Cost-Sensitive Thresholding

Total cost = 100×FN + 10×FP. Scan thresholds over [0,1] and select the minimum-cost point. Optimal thresholds used: DT=0.09, LR=0.08, NB=0.08, KNN=0.01.

Logistic Regression cost curve — LR: Cost vs threshold (optimal ≈ 0.08).

Decision Tree cost curve — Decision Tree: Cost vs threshold (optimal ≈ 0.09).

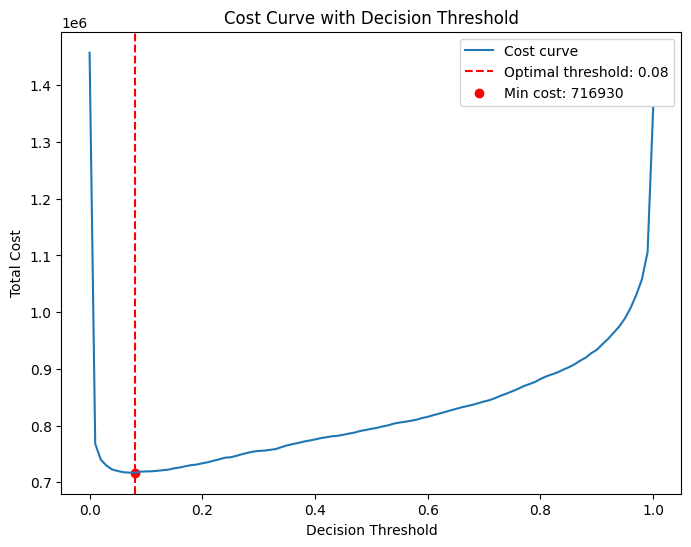
Naïve Bayes cost curve — Naïve Bayes: Cost vs threshold (optimal ≈ 0.08).

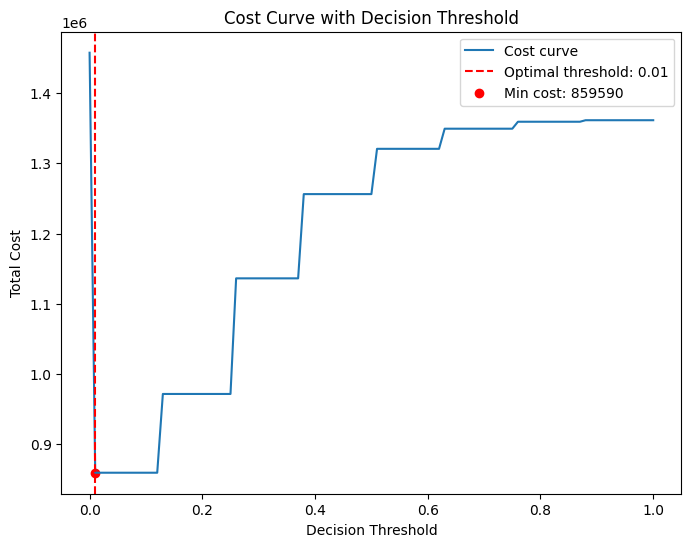
KNN cost curve — KNN: Cost vs threshold (optimal ≈ 0.01).

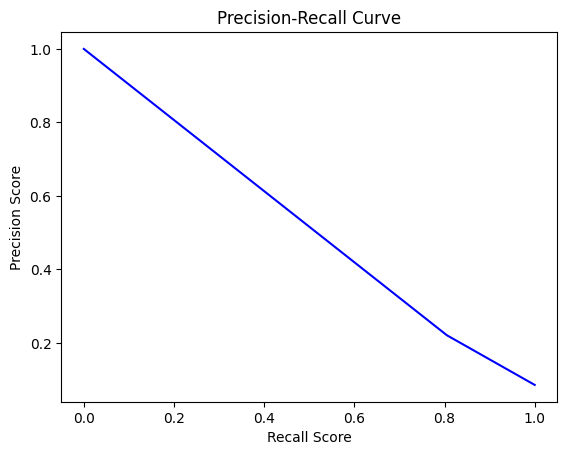
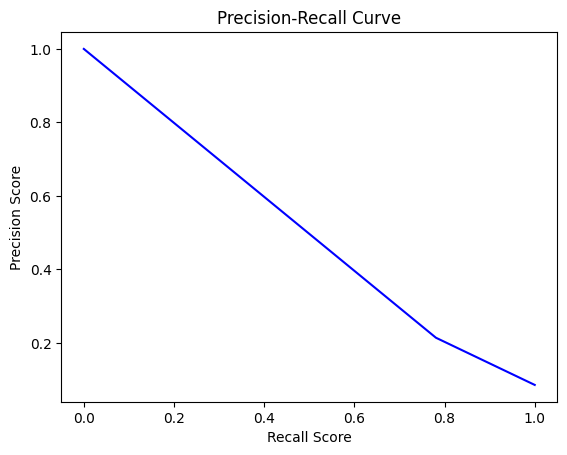
Evaluation

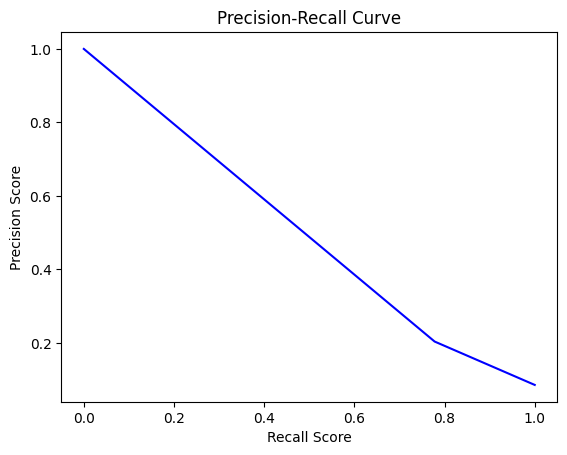
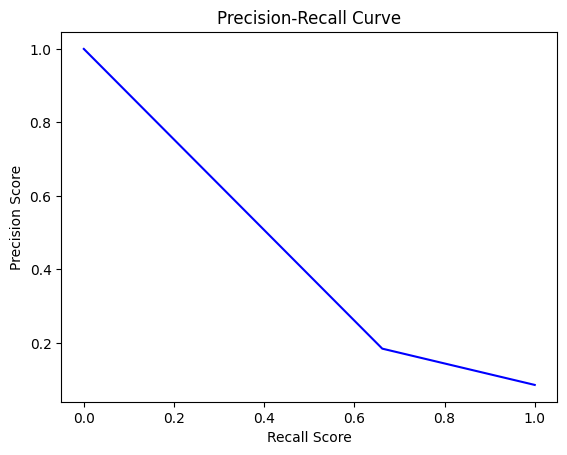
Report Accuracy, Precision, Recall, MAE, and Confusion Matrix before/after thresholding. Post-threshold, LR achieves the highest recall and lowest total cost.

Model	Opt. Threshold	Notes
Logistic Regression	0.08	Best recall & lowest cost after tuning.
Decision Tree	0.09	Competitive recall with tuning.
Naïve Bayes	0.08	High baseline recall; cost improved.
KNN (k=8)	0.01	Low threshold needed; recall trails LR.

LR PRC — Logistic Regression: Precision–Recall Curve.

Decision Tree PRC — Decision Tree: Precision–Recall Curve.

Naïve Bayes PRC — Naïve Bayes: Precision–Recall Curve.

Selected Code

Train/Test Split & Target

from sklearn.model_selection import train_test_split

y = df["_MICHD"].replace({2: 0})   # 1 = CHD/MI ever; 0 = otherwise
X = df.drop(columns=["_MICHD"])

X_train, X_test, y_train, y_test = train_test_split(
    X, y, test_size=0.40, random_state=42, stratify=y
)

Recall-Focused CV & Threshold Search

from sklearn.model_selection import GridSearchCV
from sklearn.linear_model import LogisticRegression
import numpy as np

# Logistic Regression (recall-first)
lr = LogisticRegression(penalty="l1", solver="saga", max_iter=2000)
grid = {"C": [0.5, 1, 1.4142, 2, 3]}
lr_cv = GridSearchCV(lr, grid, scoring="recall", cv=10, n_jobs=-1).fit(X_train, y_train)
lr_best = lr_cv.best_estimator_.fit(X_train, y_train)

def min_cost_threshold(y_true, proba, fn_cost=100, fp_cost=10):
    best_t, best_c = 0.5, float("inf")
    for t in np.linspace(0, 1, 501):
        yhat = (proba >= t).astype(int)
        fp = ((yhat==1) & (y_true==0)).sum()
        fn = ((yhat==0) & (y_true==1)).sum()
        c = fn_cost*fn + fp_cost*fp
        if c < best_c: best_t, best_c = t, c
    return best_t, best_c

t_opt, _ = min_cost_threshold(y_test.values, lr_best.predict_proba(X_test)[:,1])

Conclusion & Future Work

Cost-aware thresholding aligns the model with clinical priorities (catch more positives). Logistic Regression performed best after tuning. Next: calibrate probabilities, explore cost-sensitive learners and class-imbalance remedies, and validate on external cohorts.

Contents